※ 本文轉寄自 ptt.cc 更新時間: 2023-08-04 09:08:52
看板 Gossiping
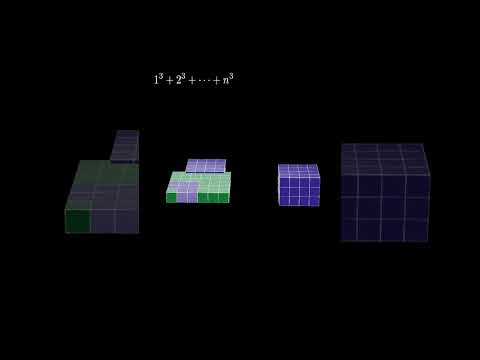
作者 標題 [問卦] 數列立方和 為什麼等於數列和平方??
時間 Fri Aug 4 05:22:14 2023
https://i.imgur.com/Vcal0Qe.jpg
![[圖]](https://i4.disp.cc/imgur/Vcal0Qe.jpg)
五歲女兒問我這個問題
我想半天
是我斷層太大 還是她跳級太快
這種算式是怎麼變到下一步的
還是說
就只是公式 沒有為什麼??
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 1.168.139.158 (臺灣)
※ 作者: assassinASHE 2023-08-04 05:22:14
※ 文章代碼(AID): #1ap1g8t5 (Gossiping)
※ 文章網址: https://www.ptt.cc/bbs/Gossiping/M.1691097736.A.DC5.html
推 : 你女兒五歲才問? 我3歲就問了欸1F 27.240.232.105 台灣 08/04 05:22
推 : 這小一的題目吧 跳級不算快2F 36.239.82.141 台灣 08/04 05:26
推 : 教他Sigma啊3F 59.115.209.139 台灣 08/04 05:27
推 : 她是科西4F 210.9.98.250 澳大利亞 08/04 05:28
→ : 你別算那麼多只看123就能推出來了啊5F 133.32.155.88 日本 08/04 05:33
推 : 把現實生活三度空間轉成二度空間 你就懂了6F 118.169.58.199 台灣 08/04 05:35
推 : 帕斯卡三角形7F 220.141.194.30 台灣 08/04 05:37
推 : 有一個小朋友問我 自然數等冪和怎麼算8F 111.246.100.204 台灣 08/04 05:40
→ : 可以用數學歸納法9F 67.168.192.176 美國 08/04 05:44
→ : 榨甘蔗沒有為什麼??10F 36.225.202.72 台灣 08/04 05:53
推 : 你有5歲女兒,而且會問這種問題,你直播11F 223.141.232.208 台灣 08/04 05:59
→ : ,窩也直播肛門榨甘蔗,笑死
→ : ,窩也直播肛門榨甘蔗,笑死
推 : 我國中才教這個。數學歸納法13F 1.162.110.196 台灣 08/04 06:01
→ : 國中有人科展是證明這個 給你參考
→ : 國中有人科展是證明這個 給你參考
→ : 國中科展證這個程度太差了吧…15F 67.168.192.176 美國 08/04 06:03
推 : 歸納法是先知道答案再來證明16F 36.225.75.131 台灣 08/04 06:08
→ : 最好有人可以一眼看出來這個公式啦
→ : 最好有人可以一眼看出來這個公式啦
推 : 天才不會拿等號兩頭跑來問你為什麼 別幻想18F 42.73.38.48 台灣 08/04 06:11
→ : 求數列和的技巧有時候就先代數字看規律啊19F 67.168.192.176 美國 08/04 06:11
推 : 當然不是純數字證明,他是用圖形之類的20F 1.162.110.196 台灣 08/04 06:18
推 : 我以為這是國小題目而已21F 39.10.73.190 台灣 08/04 06:20
推 : 數歸10行內就證完了22F 180.218.168.193 台灣 08/04 06:28
推 : 這種等號 一看就知道用數學歸納法秒解23F 1.160.154.19 台灣 08/04 06:55
推 : 幹嘛要證,直接按計算機不就好24F 70.66.225.228 加拿大 08/04 07:01
→ : 數學歸納法,不過才五歲,跟她說過11年才25F 114.140.73.93 台灣 08/04 07:08
→ : 會學
→ : 會學
推 : 五歲應該有玩骨牌了 有玩過就會了==27F 36.239.82.141 台灣 08/04 07:09
推 : 她從哪裡知道的 巧虎有教數學喔28F 1.164.81.74 台灣 08/04 07:09
→ : 就看現在小孩有沒有孩玩這種玩具29F 36.239.82.141 台灣 08/04 07:09
→ : 假如她知道1+...+n-1 = n(n-1)/2 就可以解30F 67.168.192.176 美國 08/04 07:11
→ : 釋給她聽 不過你八成是唬爛的
→ : 釋給她聽 不過你八成是唬爛的
→ : 拉馬努金投胎 抓32F 223.140.224.182 台灣 08/04 07:20
推 : 到5就不成立了33F 114.137.50.60 台灣 08/04 07:27
→ : 5也成立啊 這式子是可以證明的34F 1.160.154.19 台灣 08/04 07:29
→ : 具體來說 你知道n=1時成立 接著只要證明(
→ : n(n+1)/2)^2 + (n+1)^3 = ((n+1)(n+2)2)^
→ : 2 就結束了
→ : 具體來說 你知道n=1時成立 接著只要證明(
→ : n(n+1)/2)^2 + (n+1)^3 = ((n+1)(n+2)2)^
→ : 2 就結束了
→ : 更正等號右邊為((n+1)(n+2)/2)^240F 1.160.154.19 台灣 08/04 07:34
推 : 小孩子的話 拿立方體出來攤平比較41F 180.177.122.197 台灣 08/04 07:35
→ : 她看得到阿卡西紀錄48442F 36.226.203.250 台灣 08/04 07:51
![[圖]](https://i4.disp.cc/imgur/tcFyGXm.jpg)
推 : 用歸納法啊44F 49.216.29.145 台灣 08/04 07:52
→ : 能懂嗎45F 67.168.192.176 美國 08/04 07:52
→ : 至少五年級有機會吧
→ : 至少五年級有機會吧
推 : 就只是個公式,這是數學中很有名的147F 101.10.60.145 台灣 08/04 08:06
→ : 到n的K次方和,K等於3的時候恰好有
→ : 這麼漂亮的結果,k如果等於其他的整
→ : 數沒有這麼漂亮的結果啦。
推 : 還有數學家專門在研究這種1到n的K次
→ : 方和的公式中多項式的係數,叫做伯
→ : 努利數
→ : 到n的K次方和,K等於3的時候恰好有
→ : 這麼漂亮的結果,k如果等於其他的整
→ : 數沒有這麼漂亮的結果啦。
推 : 還有數學家專門在研究這種1到n的K次
→ : 方和的公式中多項式的係數,叫做伯
→ : 努利數
推 : 沒物理意義的東西很難用口語說明54F 101.10.107.176 台灣 08/04 08:18
→ : _(:з」∠)_
→ : 頂多就給你視覺化而已
→ : _(:з」∠)_
→ : 頂多就給你視覺化而已
--
※ 看板: Gossiping 文章推薦值: 0 目前人氣: 0 累積人氣: 158
1樓 時間: 2023-08-04 10:38:33 (台灣)
→
08-04 10:38 TW
這問題 可有趣了 傳說中的"和分"與"差分" 就是 從正整數簡單有限數列與有限級數和 計算開始 當然 二項式展開公式也要熟練一下 才能理解我40年前我小學時代 曾在當時代"高中數學課本"看到"堆垛"一詞 完全看不懂 不過要計算的東西 我很有興趣 只是我高中時就忘記這存在了 等我再次接觸時 已經30幾歲了然後 1× 2× 3× 4 + 2× 3× 4× 5 + 3× 4× 5× 6 + ......+ n× (n+1)× (n+2)× (n+3) 這道題如果沒有考試時間壓力 有足夠空閒時間 慢慢想 慢慢算 仔細算 算起來才過癮 很消磨時間又不無聊 尤其是 第一次算出答案後 再算第二次能夠找到新算法 也是一種快樂最後 問題要問的是 為何 "首項是1且公差為1的等差數列(加總每一項之和)的平方" 會等於 "首項是1且公差為1的等差數列加總(每一項的立方)之和"數列與級數 需要很嚴格定義 才不會未來被 帶歪而走火入魔
回列表(←)
分享