回上層
Disp BBS
看板 Gossiping
作者 cybergenie ((不要看這裏))
標題 Re: [新聞] 麻省理工博士數據分析 6.9萬川普選票被篡
時間 Fri Nov 13 05:53:34 2020

※ 引述《BinnigQuate (新手上路 能閃則閃)》之銘言：
: ※ 引述《goldenhill (我的人權時代)》之銘言：
: : 3.完整新聞標題:麻省理工博士數據分析 6.9萬川普選票被篡改
: : 肯特（Kent）的選票數據，呈現出非正常的散點分布，只要共和黨支持率超過20%，軟
: : 體的算法就開始自動減少川普的得票，有明顯的修改痕跡。
: 八卦是這位Shiva要在Twitter上討論這個研究，
: 可是他的Twitter帳號竟然就被封了，
: 一堆左派電視台爭相採訪他，
: 但被他拒絕了，
: 因為他知道記者訪問回去之後會怎麼誣陷他，

我想借題發揮一下之前有被提出來過，但是可能因為較為複雜所以討論的人不多。

進入正題之前，我們先來點數學：

假設我們對 0-19 之間 20 個整數作公平的隨機取樣，那麼第一個數字為 1 機會有多少？

機會大概是 55%。因為有 1 與 10, 11, ..., 19 共 11 個可能。


同理，除了 1 以外的數字，例如 2，機會有 5%。

我們也可以把範圍從 0-19 放大到 0-100，並計算第一個數字為 1-10 之間某一數字的可
能性（排除 0）。因此可以用不包括 0 的百分比作為輸入。

這就是所謂的班福特數列。這常常在會計學上用來抓數字造假的機率。例如，可以把某公
公司在一段時間內的出帳或入帳的金額。當資料愈大時，每一筆金額的特定位數字應該要
愈接近班福特數列。


來實作一下：

[圖]

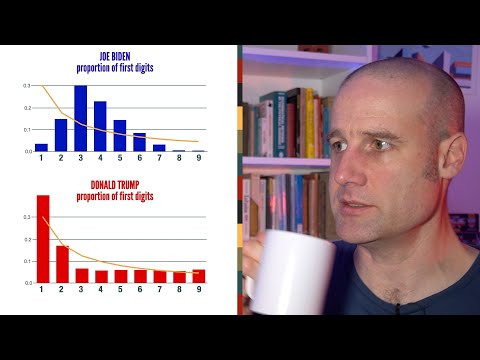
兩個數列 A, B 這次美國某區兩陣營每次開票時報出的數字中，頭位數字分部的比例。
（四捨五入過所以加起來不是 100。不過這不影響計算）

第三個數列是班福特序列。理論上 A B 都要接近 Benford。所以我們可以計算兩組數字
與 Benford 的標準差。

   stddev
A: 1.202
B: 0.699

A 與 Benford 的標準差快是 B 的兩倍。

當然，這只是一區的資料，並不能因此說 A 陣營必然有作帳。這個只能說在這區，B 陣營
的數據比 A 陣營更接近自然產生的隨機數。

不過，我們可以這個方法應用到多個區。比較看這兩個陣營在多個區中，拿到較高 stddev
的機會是不是一樣。

結果，嗯，其實跟媒體上傳出有計票誤差發生時，結果都非常剛好的有利於某特定陣營的
現像一致。

一場球賽中，發生多次裁判誤判，結果都非常剛好有利於某隊。不啓人疑竇？

我等下會給出完整証明。我先去收個 UPS..



--
→ k_______n:我推的平權政策 都不著重種族之間的平等，改強調種族之間的差別待遇年輕人都很歡迎 但就是太過激進 另外再特別給非裔專屬特權
推 w_____2:XDDD
→ D_____N:沒有種族平等還能叫做平權？？？
→ k_______n:這兩個配起來非常棒 最好是加點街頭暴力
推 j_________n:那就不算是種族平等了吧..

--
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 148.168.216.5 (美國)
※ 文章代碼(AID): #1VhQxcy- (Gossiping)
※ 文章網址: https://www.ptt.cc/bbs/Gossiping/M.1605218022.A.F3E.html
※ 同主題文章:
Re: [新聞] 麻省理工博士數據分析 6.9萬川普選票被篡改
11-13 04:24 BinnigQuate.
Re: [新聞] 麻省理工博士數據分析 6.9萬川普選票被篡改
11-13 05:53 cybergenie.
推 parsons12342: 推 不然別人以為我看不懂1F 11/13 05:55
推 laroserose:2F 11/13 05:57
推 linad: 推，讓事實證據說話...3F 11/13 05:58
推 NgJovi: 恩4F 11/13 05:58
推 ECZEMA: 快發推特啊~ 想看封號5F 11/13 06:02
推 prettychiu: 你在說benfords law想看續集6F 11/13 06:14
推 unicorn999: https://youtu.be/etx0k1nLn787F 11/13 06:23
→ ZO20: 有沒有質數版本?8F 11/13 06:26

我也想知道。不過沒辦法証明質數有總量上線

推 homer00: 不少順豐來敲門嗎？
這個不少自媒體提過了9F 11/13 06:31

大部的自媒體都只有算一半。光是看 Benford 是沒用的。
跟 Benford 比只能說特定群隨機性比較低。但不能說他一定有作票。樓下某個五毛說的沒
用應該是指這個。

推 newwu: 要有總數才能分析p值吧  這應該做goodness-of-fit 用卡方去檢測11F 11/13 06:34

對耶。是同行？

推 dash007: 好專業13F 11/13 06:34
推 serenatw: 下篇ae什麼的五毛會挖你底細以證你寫的是廢言^^14F 11/13 06:40
→ newwu: 你有多少個開票結果15F 11/13 06:40
噓 ryanworld: 一堆看不懂也在推16F 11/13 06:46
噓 diawboris: 班佛仔又出現了 查一下幾天前的文好嗎 事實查核根本
沒用 造謠仔都不看的然後一直重複PO17F 11/13 06:50
推 bakedgrass: 事實查核真的沒用阿，我已經認清了，樓上也放棄吧19F 11/13 06:51

數列本身是沒用沒錯啊。後面隨之而來的計算才有用。

不過我知道你看到「沒用」兩個字後。後面的描述就不會再看了。

然後基本上共產黨開的事實查核中心只有共產黨員會相信。跟毛語錄一樣大概。

→ newwu: 不算同行  在唸沒人要的物理系，所以準備轉DS20F 11/13 07:05

不要轉 DS 啦。若沒有 PhD 的話只能當低階碼農。物理好玩多了。

推 Asato163: 有趣推21F 11/13 07:06
推 Sniqow: 班佛定律似乎是現象 無法證明?22F 11/13 07:09

有証明啦。 好像 2006 年有論文。晚一點找找。

質數的 Benford 還沒辦法証明。我對這個很有興趣。不過前提是要知道質數是否有上限。
這個大概這一輩子是看不到了。

→ newwu: 沒辦法啊  學術路難走  物理工作大部分又不收外國人23F 11/13 07:13

會嗎？物理所外國人不少啊。除非你唸的是敏感題目？
轉的話轉 CS 輔 DS。機會大一些。加個特定專長例如 bioinformatics，就業機會大。

推 lk820: 這好像可以寫成一篇論文24F 11/13 07:13

應該是可以。我們團隊正在弄。

不過我再申明一次這方法沒辦法証明作票。只能說特定陣營票數的隨機性有可疑的空間。
作票與否那是法律問題，不是科學問題。

推 yaohwei: 是 我們可以計算兩組數字與 Benford 的差異的標準差嗎？25F 11/13 07:14

我們是計算 標準差的大小。用 euclidean distance 意思一樣。

→ newwu: 我已經快畢業了啦  是想找DS工作  學校會收外國人，我是說業界  太多物理業界的工作都和國防相關了
理論物理PhD畢業離開學校只能跑去找別的工作26F 11/13 07:21

理論物理確實路比較窄。轉 CS/DS 有空間。不過別放棄啊。有真愛才走得久。
我花很多空閒時間去計算 Black Hole Math。無耐不是本科料。算得很辛苦。

推 meRscliche: push29F 11/13 07:26
※ 編輯: cybergenie (148.168.216.5 美國), 11/13/2020 07:31:25
→ newwu: 想到這個就不爽 假如唸化學或生物資訊 都搶手多了30F 11/13 07:28
→ chordate: 額，Benford's Law的分佈是頭位數字d的機率是31F 11/13 07:28
→ newwu: 啊 用到另一個帳號了…32F 11/13 07:29

幫改。

→ chordate: Log[(d+1)/d] 你是不是把推導搞混了....33F 11/13 07:29
推 wayne1120: 推34F 11/13 07:30
→ chordate: Benford's Law是在那群數取對數的尾數是均勻分佈下成立我是沒有看到學術文章說可以用在選舉上啦...35F 11/13 07:30

嚴格來說任何隨機數都可以拿來用啦。只是現實生活中產生的數字可能不那麼俱有隨機性
就是了。

→ chordate: https://tinyurl.com/y6zrbwfb 只有看到報紙文章用在伊37F 11/13 07:31
[b]The Devil Is in the Digits: Evidence That Iran's Election Was Rigged
[圖]
Since the declaration of Mahmoud Ahmadinejad's landslide victory in Iran's presidential election, accusations of fraud have swelled. Against expectati ...

 
→ chordate: 朗選舉上，但是我認為隨便用很危險的38F 11/13 07:32

是不行沒錯。所以沒打算搭這順風車。並且我也沒說是什麼陣營隨機性比較低。

其實看新聞可以看到開票出包結果都是很剛好的有利於某營。這不用數學來算，誰都看得
出來XD

→ chordate: 除非拿很多次選舉結果都證明符合，否則不能據此說
有造假可能39F 11/13 07:33

Benford 只能証明某營開票隨機性比較低而己。那沒辦法証明造假。很多自媒體都過度解
讀這東西。選舉造假是政治司法問題。不是數學問題。

→ chordate: 不是任何隨機數都可以，上面有說了是取對數以後尾數
平均分佈才可以。
而且Benford's Law首位數字是1的機率約是0.30141F 11/13 07:41
→ newwu: 感謝啦 我本來就也喜歡cs啦 寫code很有趣44F 11/13 07:43
→ chordate: 你用的分佈我上面就說了，可能是和推導搞混了45F 11/13 07:44

有道理。來算算看。

推 zenon6414: 用歸謬法可以簡單證明質數總量沒有上限46F 11/13 07:47
→ chordate: https://tinyurl.com/y6rroty6
去看Benford的原始論文吧，556頁47F 11/13 07:47
推 VVizZ: 球是猿的49F 11/13 07:49
→ chordate: 表格有列出來。50F 11/13 07:49
推 ccufcc: 無可疑啦，哪次有可疑51F 11/13 08:04
推 wbt77hsy: 就是解釋隨機性的嘛52F 11/13 08:33
→ GYda: 恩，跟我想的差不多（?）53F 11/13 08:34
推 jonestem: 喔喔喔喔，漲姿勢了54F 11/13 08:40
推 prettychiu: 文組的大大可以看Netflix的connected裡面有一集在討論班佛！好看！55F 11/13 08:49
推 neo5277: 推唷57F 11/13 09:00
推 cerberi: 推58F 11/13 09:18
推 apple00: 就經典德國坦克問題 用繳獲的德國坦克編號推算出德國坦克總數量
誤差只有1% 一個數學家推算出來比派出上千個間諜偷出來的情報還準59F 11/13 09:18
推 LordOfCS: 推63F 11/13 09:21
推 giraffe1021: 七樓po的影片其實就說的蠻清楚了 選舉中不一定成立這篇論文也直接表明Benford’s law在選舉中問題很多無法拿來判斷一場選舉是否做票
https://doi.org/10.1093/pan/mpr01464F 11/13 10:04

Benford's Law 能不能看出有沒有作票？答案肯定是不行。
但是我認為用來研究兩方之間哪一方的隨機性比較大是可以的。

當然隨機性比較低也不能說就一定是有問題。例如 49% - 51%。

若兩方都是用一樣方法，但在絕大部份地區都顯示其中一方隨機性比較低，這很難說不可
疑吧？

推 nonedude: 那如果是把原始b的數轉給a那這樣不就兩邊的班佛數都異常？！68F 11/13 10:21
推 chiuvv520: 數據會說話 數據問題提出懷疑不是就科學假設 還是大部分人都只看結果70F 11/13 10:47

很多人一看班佛＋美國選舉，直接就說不行不可信了。
又知道我算的是選舉中的什麼東西了？

→ BANDITCS: 在美國敏感領域真的大部分只能在學界...業界身分要求很多...不過也不是不可能，需要一點運氣72F 11/13 11:02
推 nalthax: 推，但是這麼細膩的立論與檢證，在台灣的話應該不會被當成可採納的事實或證據74F 11/13 11:36
推 psynanako: 幫推76F 11/14 00:16
※ 編輯: cybergenie (148.168.216.5 美國), 11/14/2020 03:29:01

--
--
(cybergenie.): Re: [新聞] 麻省理工博士數據分析 6.9萬川普選票被篡改 - Gossiping板